浅谈弹性与碰撞:从小球的反弹看碰撞的奥秘
2023年11月1日
前一阵子我们学牛顿定律相关知识的时候,经常遇到小球从某一高度下落做自由落体运动,掉到地面上,然后反弹的情景题。有些题的设定是完全弹性碰撞,小球反弹后将回到原来的高度。而实际情况是小球弹起后高度发生了衰减。一般来说,不同的小球和不同的地面发生碰撞,弹起的高度和次数一般不同,高度衰减的程度也是不一样的,但我相信这种衰减必然存在着相似的规律,即可以通过合理的建模,来预测某种材质的小球在第x次与某种材质的地板碰撞后弹起的高度h。
这让我想到,一年前,我曾在家中做过非常类似的实验——用家中不同的小球(乒乓球,弹性球,玻璃球等等)和不同质地的地板(木板,瓷砖,地毯等)进行自由落实验,并得到了大量数据。当时在几次失败的建模尝试后,最终我得到了较好符合实验数据的模型,经过理论分析也是正确的。可以说这既是一次成功的物理探究,也是我第一次进行数学建模的尝试。
下面是复现实验和建模的过程,并分析其背后的原因。
去年年末由于疫情待在家中,实验条件非常简陋,唯一的测量仪器是手机相机和尺子。由于小球会在水平方向上受到随机扰动而产生不小的位移,小球总会跑到画面外面,想要通过手机录像和尺子配合记录小球每次弹起的准确高度h是不太可能的。于是我决定做一下改动,探究小球弹起的时间t与已经碰撞的次数x(以下称弹跳序数)的关系,这样就可以不用尺子,将手机摄像头一直对准小球。如果探究出t-x关系,通过位移-时间公式,高度h与x的关系也将是明了的。
然而,查看手机录像发现,所测的时间的精度还是差了一些,于是我用慢动作录像(事先测量了慢动作视频时间流逝的速度和现实时间之比)反推出真实的时间,测量精度一下就上来了。(当然由于掐表掐的不准,还是由一点点误差)。在不同的时间我做了多组实验,这是第一次实验记录。
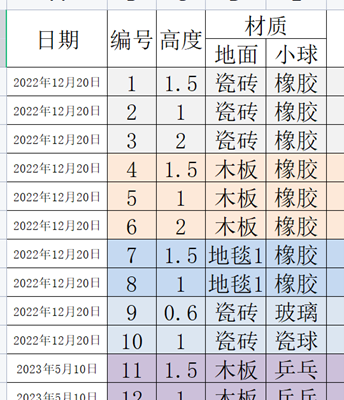
在得到这些实验的数据后,我进行了三次建模。
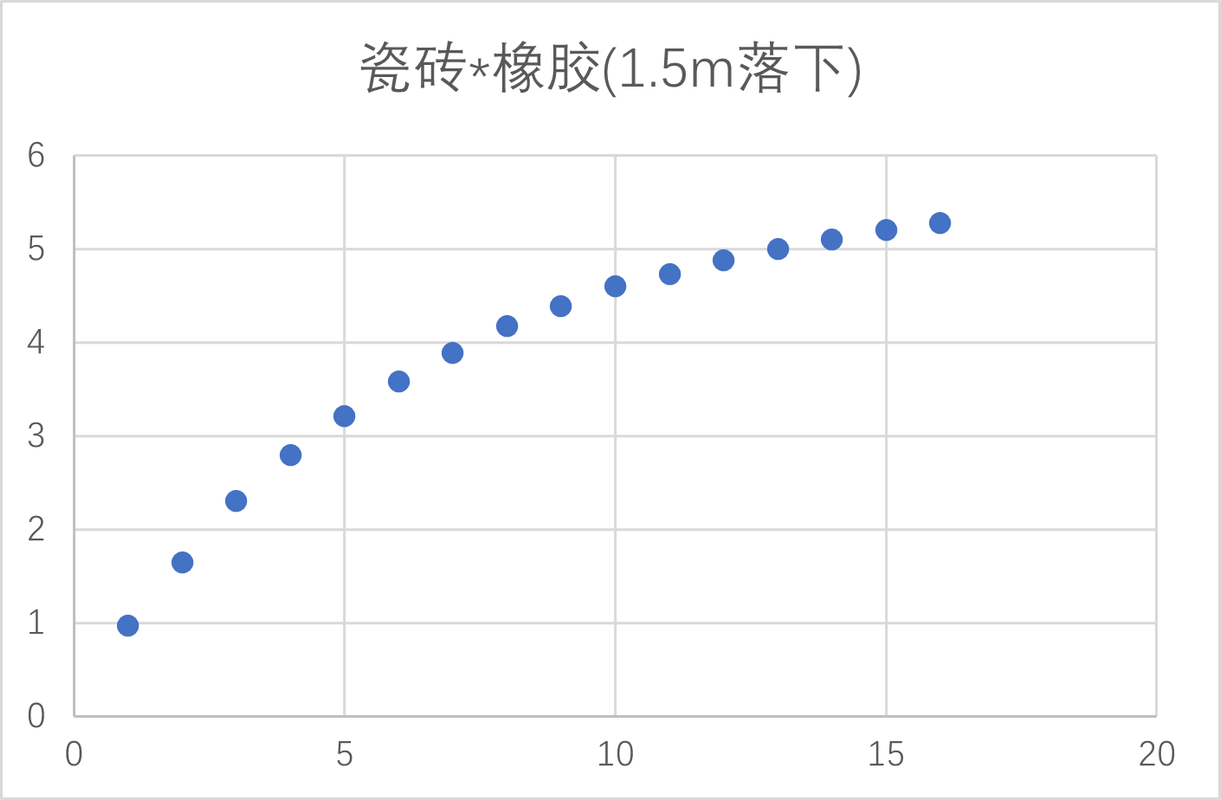
可以想到,在实验得到的直接数据中,所测得的时间并不是第$x$次和下一次两次落地的时间差,而是小球第$x$次落地与第一次落地的时间差。第一个模型直接将这个时间作为$t$。第一个实验(橡胶小球从$1.5m$高度落向瓷砖)图像如上图所示。由于存在高度衰减,$t$与序数$x$的关系并不是线性的,而是这样向上凸的。
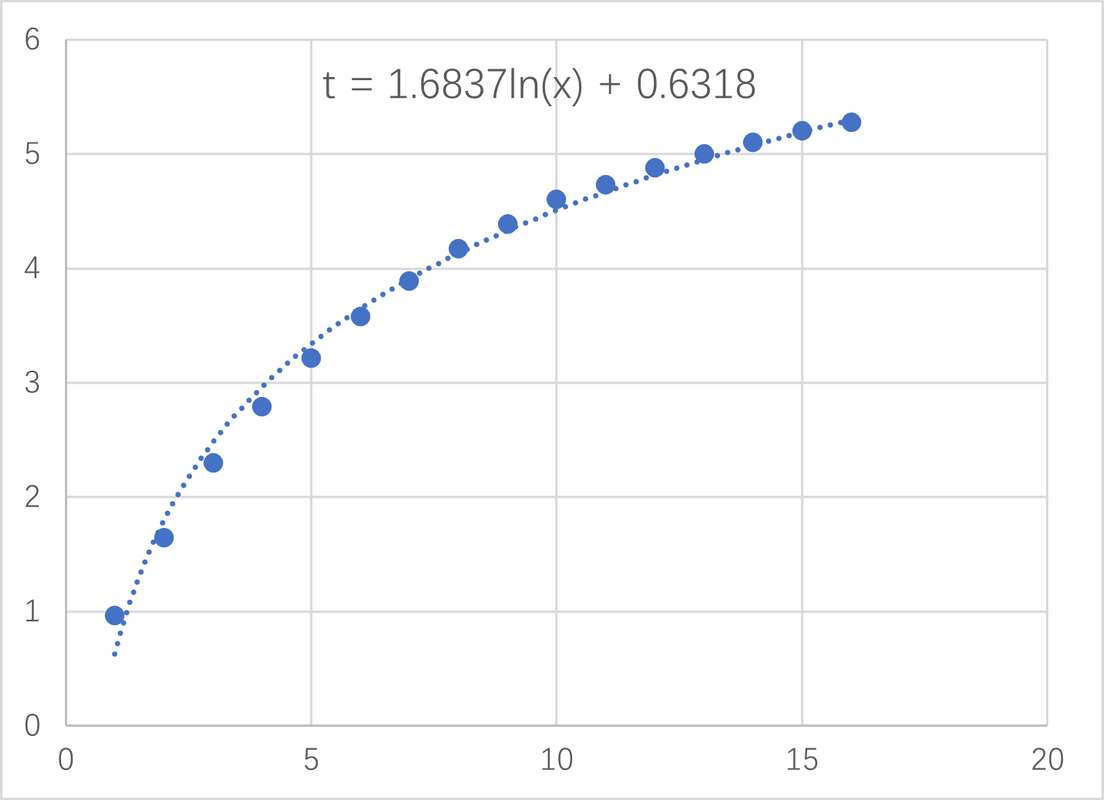
也许是被直观的印象冲昏了头脑,我不假思索的认为,上面的图像就是对数函数没错,直接进行拟合。巧合的是,对于这次实验,$\ln$函数竟然拟合的很好(如下图1所示),然后我更加坚信这是对数函数,并直接得到结论:
小球第$x$次与第一次落地的时间差$t$与$x$的关系是$$t=k\ln x+b$$
k和b是只由小球、地板材质直接确定的系数。
对于第一次实验,$k=1.6837,b=0.6318$。
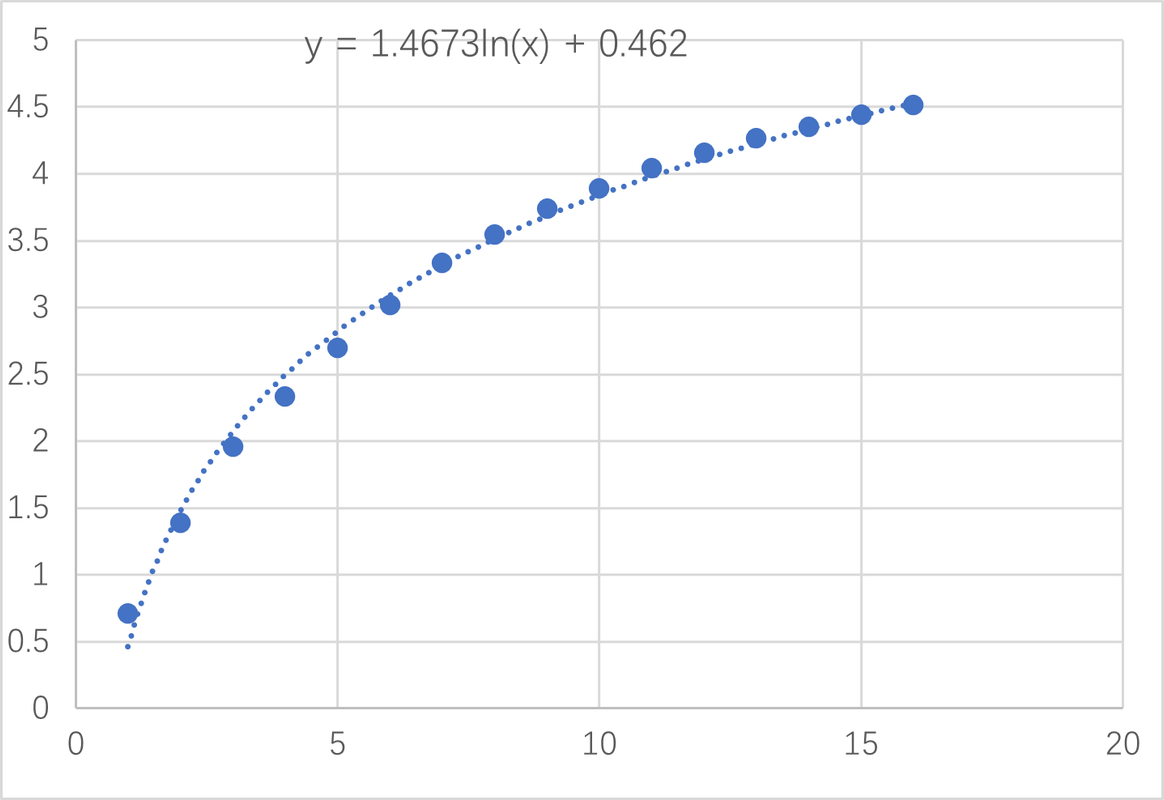
如果这个结论是对的($k$和$b$是只由材质确定的系数),那么如果第二次实验只更改了下落的高度,所测的$k$和$b$应当和上面的值相同。然而下面第二次实验(下落高度改成$1m$)(下图2)拟合的结果显示:
$$k= 1.4673,b= 0.462$$
这显然与上面的结果有很大的不同。如果认为这是误差的话,第三次实验($h=2m$)的结果$k=1.898,b=0.6809$又如何解释?
如果按我现在的想法,这$k$和$b$的不同直接就可以宣判这个模型的死刑,可以研究更好的模型了。可我当时还不死心,也许是因为$\ln$函数对每个图象单独都契合的特别好,只是每次实验的系数$k、b$都不一样罢了。我偶然注意到k和b似乎隐约与高度h存在线性关系,如果设
$$k=oh+p,b=qh+r$$
并反解出$o、p、q、r$四个参数的话,这个模型还有成立的可能。
通过尝试,我得到以下拟合数据:

这样,就由确定的材料(瓷砖,小球)确定了四个参数$o、p、q、r$,进而可以得到与每个下落高度对应的k和b,然后就有$t=k\ln x+b$,且契合度很高。
终于,当这个模型“大功告成”的时候我才意识到不对,两个物体怎么会有四个参数!而且结论是这个鬼样子:
-
小球第x次与第一次落地的时间差$t$与$x$的关系是$t=k\ln x+b$
-
$k$和$b$是由$o、p、q、r$四个参数确定的系数,$o、p、q、r$由两个材料确定,它们的物理意义不明
四个参数构成了这么复杂的模型,每个参数的物理意义不知道,他们体现不出来材质的任何性质。最要命的是,凭什么最后的函数结果就是ln,其原因是什么,仅仅是因为图像长得像?
种种疑问浮现。这时候我想到,其实ln是个连续的函数,而我得到的实验数据本质是是离散的,是数列,ln即使拟合的再好,由于性质的不同,图像也根本不可能是ln。因此我决定废弃这第一个模型,不仅是因为不合理的ln函数,它缺失也确实物理的简洁美。
第二个模型中,我假设总时间t的平方和序数x、下落高度h成正比,则可以写成$t=p\sqrt{hx}$,$p$是材质确定的参数。虽然更加简洁,但这样误差较大,且无法给出完全弹性碰撞的p值(此时t与x直接成正比了,不符合$t=p\sqrt{hx}$,找不到$p$是自然的),因此也被抛弃了。
下面来重点叙述第三个模型。
第三个模型
此时我意识到,若把小球第$x$次与第一次落地的时间差当成$t$来研究会遇到很大的困难,因此改用某次弹起与下次弹起的时间间隔作为$t$,这样,每一次反弹的序数$x$对应了不同的$t$,因此$t$是$x$的函数,记作$t(x)$。(由于$x$是正整数,$t$也是一个数列。)
那么,经过简单的作差,第一次实验的图像将被改写成这样:
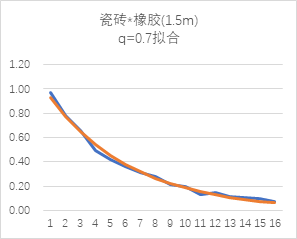
(弯弯曲曲的折线是我掐表不准造成的)
为了解释曲线,我假设每次碰撞弹跳高度缩短的比率是恒定的,即小球每次弹起的高度$h(x+1)$与$h(x)$的之比恒为$q$,$0<q<1$,$q$是由材质确定的参数。所以第x次弹起的高度h(x)与原高度h的关系应当是$h(x)=h·qx$,则根据公式$t(x)=2\frac{\sqrt{2h(x)}}{g}$,把$h(x)=h·q^x$带入,就有:
$$t(x)=2\frac{\sqrt{2h·q^x}}{g}$$
当$q=0.7$时,第一个实验的拟合函数契合度最好。
对于第二个实验(材质不变,高度$1m$)和第三个实验($2m$),都可以得到相同的$q$值$0.7$:
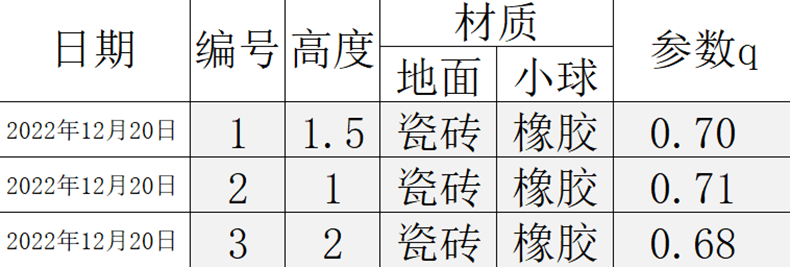
这说明,$q$确实是由只由材质确定的,与下落高度无关的一个数,姑且称为“材质参数”。为了进一步检验,其他实验我也陆续得到了$q$值:
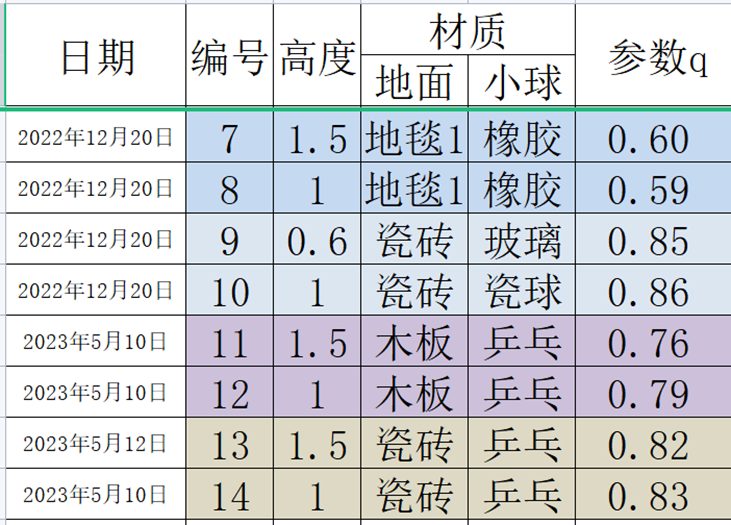
(相同的材料相同的颜色)
可以发现,不同下落高度下,相同材质间q值近似相等,q确实与下落高度h无关。我猜测其与碰撞的恢复系数有关。当$q=1$时,t恒等于$2\sqrt{\frac{2h}{g}}$,这个弹跳过程就是完全弹性碰撞。可以总结出以下两点:
-
参数$q$与材质的光滑程度(或硬度)呈正相关,瓷砖*玻璃组合最光滑(硬),因此$q$最大。这些都是材质的固有性质,所以对于给定的材料,$q$值不变。
-
从碰撞角度考虑,有这样的结论:
$$q=\frac{h(x+1)}{h(x)}$$
$$h∝v^2 \Rightarrow q=e^2$$
$$e=\frac{v(x+1)}{v(x)}$$
其中$e$是碰撞恢复系数。可知我引入的“材质参数”$q$其实是两材质间的碰撞恢复系数e的平方,二者都无量纲。那么我做的这个实验其实也是一种测量恢复系数的方法。
分析可知,我所做的所有实验以及一切资料都表明,在一定条件下、一定精度内,对于给定的两个物体,碰撞恢复系数$e$(或者它的平方“材质参数”$q$)是一个常数。
其原因是什么呢?当时我没有研究,认为这是自然而然的。而现在我觉得这件事情可以继续琢磨。
继续琢磨
我们知道,如果一个碰撞过程不是完全弹性碰撞,就会有机械能损失,下面将从机械能损失的角度分析。
碰撞过程中,物体受到挤压产生形变,从而产生弹力,弹力是弹性材料每一处“应力”的累积。理想弹簧的弹力满足胡克定律$F=-kx$,其他的弹性材料也近似满足胡克定律,但这只是近似,并不是严谨的。因为在碰撞过程中,弹性物质内部类似纤维束的结构发生断裂,机械能会部分转化为内能。这种转化比较微弱,真正对机械能损失影响较大的是“加载”(受压逐渐增大)和“卸载”(压力逐渐消失)过程中产生的耗散能,其产生原理是弹性材料内部的摩擦将机械能耗散为内能。
耗散能由弹性材料加载、卸载过程中的滞回曲线决定。下图是理想橡胶材料的滞回曲线,其纵坐标是应力F,横坐标是拉伸量x,可以看出它们并不像胡克定律那样是简单的线性关系,在加载、卸载过程对应的曲线中间包围了一定的面积,这个面积就是耗散能。弹性滞回现象是物理学中常见的现象,下面将通过简单的例子说明弹性滞回现象:
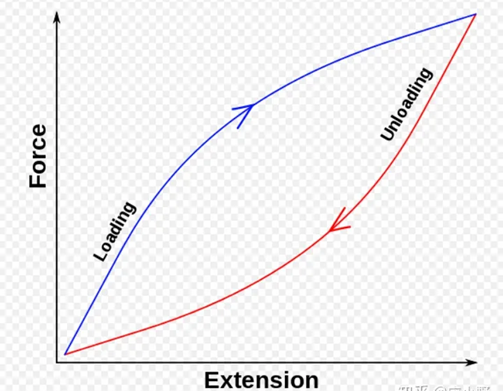
橡皮筋顶部固定在钩子上,底部逐渐挂钩码(加载),橡皮筋就会变长。随着更多的钩码被加载到其上,橡皮筋将继续延伸。当钩码被一一取下时,带子会随着受力的减小而变短。
橡皮筋不完全遵守胡克定律,可以看出其在加载时比卸载时的劲度系数k更大。在时间上,当橡皮筋卸载时,其发生形变会滞后于其受力的变化,因为长度变化需要时间,其尚未达到在加载时受到同样拉力时的长度。因此,在受到相同的力时,其在减重(卸载)时的长度比其在受压(加载)时的长度要长那么一点,在上图划一道水平线就清楚了。这会导致橡皮筋在加载时需要的能量比卸载时要多,多余的能量作为内能散失,这就是耗散能。
资料显示,我的实验中使用的小球、地板的材质——花岗岩/大理石等岩石,以及橡胶、玻璃等材料都会表现出明显的弹性滞后现象。因此,可以用上面的理论简单分析一下实验。由上图可知,曲线包围的面积即它们产生的耗散能E耗散应当正比于横坐标(拉伸量x)的平方,即$E_{耗散}∝x^2$。由于碰撞时发生的挤压使得动能转化为弹性势能,$x^2∝v^2$,由此可知$E_{耗散}∝E_k$。因此
$$E_k-E{耗散}∝E_k, v(n+1) ∝v(n)$$
(平方亦成正比),比例系数就会一个常数,这就是$e$或者$q$是个常数的原因。当然,这一证明并不十分严谨,也没法十分严谨。$e$是不是一个严格由材料固定的常数,有谁能说清呢?
更进一步的研究也超出了我目前的能力范围,这次探究就到这里结束吧,我们从一次实验出发一步步建模分析,从碰撞反弹遵循什么样的规律到它为什么遵循这样的规律一步步探明,目前的结论:小球与地面的碰撞总满足其恢复系数e是常数;实验也验证了这一点,那么我们就应该相信结论是可靠的。
参考资料
https://zhuanlan.zhihu.com/p/529087013
https://zhuanlan.zhihu.com/p/50912479
https://www.zhihu.com/question/515204780
 蓝色奇夸克
蓝色奇夸克